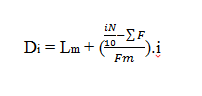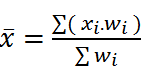UKURAN GEJALA PUSAT DATA YANG SUDAH DIKELOMPOKKAN

Ukuran gejala pusat merupakan suatu bilangan yang menunjukkan sekitar dimana bilangan - bilangan yang ada dalam kumpulan data, oleh karenanya ukuran gejala pusat ini sering disebut dengan harga rata-rata. Harga rata-rata dari sekelompok data itu diharapkan dapat diwakili seluruh harga-harga yang ada dalam sekelompok data itu.

A. Mean ( Rata-Rata Hitung )

      Dalam istilah sehari – hari, mean dikenal dengan sebutan angka rata – rata, ada dua macam mean yang di bicarakan yaitu : mean untuk data yang tidak dikelompokkan dan mean untuk data yang dikelompokan. Mean adalah total semua data dibagi jumlah data. Mean digunakan ketika data yang kita miliki memiliki sebaran normal atau mendekati normal (berbentuk setangkup, nilai yang paling banyak berada ditengah dan makin besar semakin sedikit, makin kecil makin sedikit pula, nilai-nilai ekstrim yang besar maupun yang kecil hampir tidak ada).

B. Median (Nilai Tengah)

Ukuran pemusatan yang menempati posisi tengah jika data diurutkan menurut besarnya. Median adalah nilai yang berada ditengah-tengah data setelah diurutkan dari yang terkecil sampai terbesar. Median cocok digunakan bila data yang kita miliki tidak menyebar normal atau memiliki nilai yang berbeda-beda secara signifikan.

C. Modus ( Data Yang Sering Muncul )

Modus adalah suatu angka atau bilangan yang paling sering terjadi / muncul tetapi kalo pada data distribusi frekuensi interval modus terletak pada frekuensi yang paling besar.

D. Kuartil 

Kuartil adalah suatu harga yang membagi histogram frekuensi menjadi 4 bagian yang sama, sehingga disini akan terdapat 3 harga kuartil yaitu kuartil I ( K1), kuartil II (K2) dan kuartil III (K3), dimana harga kuarti II sama dengan harga median.

E. Desil

Untuk kelompok data dimana n ≥ 10, dapat ditentukan 9 nilai bagian yang sama, misalnya D₁, D₂, … Q₉, artinya setiap bagian mempunyai jumlah observasi yang sama, sedemikian rupa sehingga nilai 10% data/observasi sama atau lebih kecil dari D₁, nilai 20% data/observasi sama atau lebih kecil dari D₂, dan seterusnya. Nilai tersebut dinamakan desil pertama, kedua dan seterusnya sampai desil kesembilan.

F. Persentil

Untuk kelompok data dimana n ≥ 100, dapat ditentukan 99 nilai, P₁, P₂, … P₉₉, yang disebut persentil pertama, kedua dan ke-99, yang membagi kelompok data tersebut menjadi 100 bagian,masing-masing mempunyai bagian dengan jumlah observasi yang sama, dan sedemikian rupa sehingga 1% data/observasi sama atau lebih kecil dari P₁, 2% data/observasi sama atau lebih kecil dari P_2.

UKURAN GEJALA PUSAT DATA BELUM DI KELOMPOKKAN

Ukuran Gejala Pusat Data Belum di Kelompokkan

Ukuran pemusatan data yang termasuk ke dalam analisis statistika deskriptif adalah rata-rata hitung (mean), median, modus, dan fraktil (kuartil, desil, persentil).

    A.  Rata-rata Hitung (Mean)

Rata-rata hitung adalah nilai yang mewakili sekelompok data.

R_H = F_i  .  X_i  / F_i = (F₁ . X₁ + F₂ . X_{2............}F_{k .} X_k  / F₁ + F_{2 ...........}F_k)

F_i = frekuensi

X_i = titik tengah

 

Contoh:

B. Rata – Rata ukur

Rata-rata Ukur/Geometri dari sejumlah N nilai data adalah akar

pangkat N dari hasil kali masing-masing nilai dari kelompok

tersebut.

G = NÖ X1. X2 . … XN atau

log G = (Σ log Xi) / N

Contoh:

   C. Rata – Rata Harmonis

Rata-rata Harmonis dari seperangkat data X1, X2, …, XN adalah kebalikan

Rata-rata hitung dari kebalikan nilai-nilai data.

RH = N

Contoh:

    D.Rata-rata tertimbang

Rata-rata tertimbang/terbobot (weighted average) adalah rata-rata yang dihitung dengan memperhitungkan timbangan/bobot untuk setiap datanya. Setiap penimbang/bobot tersebut merupakan pasangan setiap data.Rumus rata-rata tertimbang/terbobot adalah sebagai berikut :

Contoh:

    E. Median

Median (M_e) adalah nilai data yang terletak di tengah-tengah suatu data yang diurutkan (data terurut).

     -)     Jika banyak data ganjil maka :

      

        

        Contoh:

S   

      -)  Jika banyak data genap maka:

a        

            Contoh:

   F.Modus

Modus merupakan nilai data yang memiliki frekuensi terbesar atau    nilai data yang  paling sering muncul. Modus ( Sering Muncul / Data frekuensi paling tinggi)

 Contoh :

      

   G.Kuartil  

Pada prinsipnya, pengertian kuartil sama dengan median. Perbedaanya hanya terletak pada banyaknya pembagian kelompok data. Median membagi kelompok data atas 2 bagian, sedangkan kuartil membagi kelompok data atas 4 bagian yang sama besar, sehingga akan terdapat 3 kuartil yaitu kuartil ke-1, kuartil ke-2 dan kuartil ke-3, dimana kuartil ke-2 sama dengan median:

Contoh:

    H. Desil

Desil adalah Fraktil yang membagi seperangkat data menjadi sepuluh

bagian yang sama.

Contoh:

   I. Persentil

Persentil adalah Fraktil yang membagi seperangkat data menjadi seratus

bagian yang sama.

Contoh:

  Cara Mudahnya

   1.   Klik data -> data analysis

  2.   Klik descriptive statics -> ok

  3.   Pilih yang seperti sudah ditandi dikotak tersebut, dan centang summary nya dan  sebelumnya kita membuat datanya dahulu lalu muncul seperti dibawah ini

      -    Buat dahulu data seperti dibawah lalu blok semua dan pilih seperti yang ditandai dikotak merah itu

  4.   Lalu pilih seperti yang ditandai dikotak merah itu  -> klik sembarang kemudian muncul seperti tampilan dibawahnya yang gambar ke 2 lalu klik saja seperti yang ditandai dikotak merah   -> lalu klik ok saja

  5.   Lalu munculah tampilannya seperti ini 

STATISTIKA

DISTRIBUSI FREKUENSI

PENGERTIAN DISTRIBUSI FREKUENSI     

Distribusi Frekuensi adalah yang merupakan penyusunan data ke dalam kelas-kelas tertentu dimana setiap individu/item hanya termasuk kedalam salah satu kelas tertentu saja. (Pengelompokan data berdasarkan kemiripan ciri). Tujuannya untuk mengatur data mentah (belum dikelompokan) ke dalam bentuk yang rapi tanpa mengurangi inti informasi yang ada. 

Distribusi Frekuensi Numerikal adalah Pengelompokkan databerdasarkan angka-angka tertentu, biasanya disajikan dengan grafik histogram.

Distribusi Frekuensi Katagorikal adalah Pengelompokkan data berdasarkan kategori-kategori tertentu, biasanya disajikan dengan grafikbatang, lingkaran dan gambar.

Istilah-istilah Dalam Distribusi Frekuensi.

1. Class (kelas) adalah penggolongan data yang dibatasi dengan nilai terendah dan nilai tertinggi yang masing-masing dinamakan batas kelas.
2. Class interval/ Panjang Kelas/ lebar kelas merupakan lebar dari sebuah kelas dan dihitung dari pernedaan antara kedua tepi kelasnya.
3. Mid point/ Class Mark/ Titik tengah merupakan rata-rata hitung dari kedua batas kelasnya atau tepi kelasnya

TAHAP-TAHAP PENYUSUNAN DISTRIBUSI FREKUENSI

• Menghitung jumlah data 
• Mencari data tertinggi dan terendah
• Menentukan Range (jangkauan) : Selisih antara nilai yang terbesar dengan nilai yang terkecil. R = Xmax - Xmin
• Menentukan banyaknya kelas dengan mengunakan rumus Sturges K= 1 + 3.3 log N dimana K= banyaknya kelas dan N= seluruh jumlah data yang di observasi
• Menentukan interval kelas : I= R/K
• Menentukan batas-batas kelas :

           TBK = BBK - 0.5 ( Skala Terkecil )

           TAK = BAK + 0.5 ( Skala Terkecil ) 

• Menentukan titik tengahnya :

           ½ ( Batas Atas kelas + Batas Bawah Kelas )

• Memasukan data kedalam kelas-kelas yang sesuai dengan memakai sistem Tally atau Turus
• Menyajikan distribusi frekuensi : isi kolom frekuensi sesuai dengan kolom Tally/Turus

      Contoh Kasus :

  Diketahui data metah (belum dikelompokan) nilai ujian statistik 50 Mahasiswa sebagai berikut

50	58	62	77	78	32	44	43	56	54
100	55	56	78	89	77	78	64	56	43
66	67	87	67	45	56	99	43	33	34
87	90	87	78	87	64	54	43	66	57
44	55	45	65	75	43	45	56	76	87

 

Data Terkecil = Xmin = 10

Data tersebar = Xmax = 100

Range, R  = Xmax – Xmin

R = 100 - 10 = 90

Banyaknya kelas dengan rumus STURGES :

K = 1 + 3,3 log N

K = 1 + 3,3 log 50

K = 6,6 = 7

Interval Kelas :

I = R / K = 90 / 7 = 12,85 dibulatkan menjadi 13

Tabel Distribusi Frekuensi

					Tepi	Tepi	Titik	Sistem
			Batas	Bata	Bawah	Atas	Tengah=	Tally
Kelas		Nilai	Bawa	Atas	Kelas	Kelas	1,2	atau	Frekuensi
		Statistik	Kelas	Kelas	(TBK)=	(TAK)=	(BBK+BAK)	Turus
			(BBK)	(BAK	BBK-0.5	BAK+0.5
1		30 - 39	30	39	29,5	39,5	34.5	III	3
2		40 - 49	40	49	39,5	49,5	44.5	IIIII IIII	9
3		50 - 59	50	59	49,5	59,5	54.5	IIIII IIIII I	11
4		60 - 69	60	69	59,5	69,5	64.5	IIIII III	8
5		70 - 79	70	79	69,5	79,5	74.5	IIIII III	8
6		80 - 89	80	89	79,5	89,5	84.5	IIIII I	6
7		90 - 100	90	100	89,5	100,5	95	III	3

Pembuatan Distribusi Frekuensi dan Histogram dengan Excel

  Langkah-langkahnya sebagai berikut: 

1.  Klik Menu Data -> Analysis

2. Klik Histogram -> OK

3. Lalu muncul gambar dibawah ini, lalu ceklis yang seperti dibawah ini lalu klik OK 4. Lalu muncul histogram sebagai berikut

	Frequency	Cumulative %	39	Frequency	Cumulative %
49	13	26.00%	49	13	26.00%
59	12	50.00%	59	12	50.00%
69	8	66.00%	69	8	66.00%
79	8	82.00%	79	8	82.00%
89	6	94.00%	89	6	94.00%
100	3	100.00%	100	3	100.00%
More	0	100.00%	More	0	100.00%